ポリゴンメッシュをワイヤーフレームだけにする (スクリプト)
ポリゴンメッシュのワイヤーフレームだけをジオメトリとして残すためのスクリプトです。
エッジベベルを使用してエッジ部分だけを残す手順では、非平面が含まれるとうまく処理できない場合が多いです。
ブラウザでポリゴンメッシュを選択し、以下のスクリプトを実行すると、
指定の幅のワイヤーフレームをジオメトリとして生成します。
import numpy
import math
scene = xshade.scene()
# -----------------------------------------------.
# 指定のポリゴンメッシュで、面に属さない頂点を削除.
# -----------------------------------------------.
def cleanupMeshVertices (shape):
# 面で参照される頂点を取得.
versCou = shape.total_number_of_control_points
facesCou = shape.number_of_faces
vUsedList = [0] * versCou
for fLoop in range(facesCou):
f = shape.face(fLoop)
vCou = f.number_of_vertices
for i in range(vCou):
vUsedList[ f.vertex_indices[i] ] = 1
# 参照されない頂点を削除.
shape.begin_removing_control_points()
for i in range(versCou):
if vUsedList[i] == 0:
shape.remove_control_point(i)
shape.end_removing_control_points()
# -----------------------------------------------.
# 2つの直線の交点を計算。 (x, y, z)の要素のZは0.0とする.
# pA1 - pA2 と pB1 - pB2 の直線交点を計算する.
# -----------------------------------------------.
def calcLinesCrossPos (pA1, pA2, pB1, pB2):
dV = (pA2[1]-pA1[1]) * (pB2[0]-pB1[0]) - (pA2[0]-pA1[0]) * (pB2[1]-pB1[1])
if math.fabs(dV) < 1e-5:
return pA2
d1 = pB1[1] * pB2[0] - pB1[0] * pB2[1]
d2 = pA1[1] * pA2[0] - pA1[0] * pA2[1]
fx = d1 * (pA2[0] - pA1[0]) - d2 * (pB2[0] - pB1[0])
fx /= dV
fy = d1 * (pA2[1] - pA1[1]) - d2 * (pB2[1] - pB1[1])
fy /= dV
# ラフにクリッピング.
fMinX = min(min(min(pA1[0], pA2[0]), pB1[0]), pB2[0])
fMaxX = max(max(max(pA1[0], pA2[0]), pB1[0]), pB2[0])
fMinY = min(min(min(pA1[1], pA2[1]), pB1[1]), pB2[1])
fMaxY = max(max(max(pA1[1], pA2[1]), pB1[1]), pB2[1])
dx = (fMaxX - fMinX) * 0.5
dy = (fMaxY - fMinY) * 0.5
fMinX -= dx
fMaxX += dx
fMinY -= dy
fMaxY += dy
if fx < fMinX or fx > fMaxX or fy < fMinY or fy > fMaxY:
return pA2
return numpy.array([fx, fy, 0.0])
# -----------------------------------------------.
# 頂点座標の配列から、バウンディングボックスサイズを計算.
# -----------------------------------------------.
def calcBondingBoxSize (versList):
if len(versList) == 0:
return [0.0, 0.0]
minX = maxX = versList[0][0]
minY = maxY = versList[0][1]
for p in versList:
minX = min(minX, p[0])
maxX = max(maxX, p[0])
minY = min(minY, p[1])
maxY = max(maxY, p[1])
return [maxX - minX, maxY - minY]
# -----------------------------------------------.
# ポリゴンメッシュをワイヤーフレームに変換.
# -----------------------------------------------.
def convMeshToWireframe (shape, lineWidth):
if shape.type != 7: # ポリゴンメッシュでない場合.
return None
shape.setup_plane_equation()
zUpNormal = numpy.array([0.0, 0.0, 1.0])
fMinDist = 1e-5
faceOrgIndicesList = []
newVersList = []
facesCou = shape.number_of_faces
versCou = shape.total_number_of_control_points
for fLoop in range(facesCou):
faceD = shape.face(fLoop)
fvCou = faceD.number_of_vertices
if fvCou <= 2:
continue
# (x,y,z)が面法線相当.
fNormal = shape.get_plane_equation(fLoop)
# 頂点座標を一時格納.
vIndices = faceD.vertex_indices
versIndices = []
vers = []
fCenterPos = numpy.array([0.0, 0.0, 0.0])
for i in range(fvCou):
p = shape.vertex(vIndices[i]).position
p = numpy.array([p[0], p[1], p[2]])
fCenterPos += p
vers.append(p)
versIndices.append(vIndices[i])
fCenterPos /= float(fvCou)
# 法線座標系への変換行列。Z軸方向を法線とする.
xV = numpy.array([0.0, 0.0, 0.0])
minLenV = -1.0
for i in range(fvCou):
xV = vers[(i + 1) % fvCou] - vers[i]
lenV = numpy.linalg.norm(xV)
if minLenV < 0.0 and lenV > fMinDist:
xV /= lenV
minLenV = lenV
break
if minLenV < 0.0:
continue
normalV = numpy.array([fNormal[0], fNormal[1], fNormal[2]])
fnMatrix = numpy.matrix(numpy.identity(4))
yV = numpy.array([0.0, 0.0, 0.0])
zV = normalV
xV = numpy.cross(normalV, xV)
yV = numpy.cross(normalV, xV)
lenV = numpy.linalg.norm(xV)
if lenV == 0.0:
continue
xV /= lenV
lenV = numpy.linalg.norm(yV)
if lenV == 0.0:
continue
yV /= lenV
fnMatrix[0, 0] = xV[0]
fnMatrix[0, 1] = xV[1]
fnMatrix[0, 2] = xV[2]
fnMatrix[1, 0] = yV[0]
fnMatrix[1, 1] = yV[1]
fnMatrix[1, 2] = yV[2]
fnMatrix[2, 0] = zV[0]
fnMatrix[2, 1] = zV[1]
fnMatrix[2, 2] = zV[2]
fnMatrixInv = fnMatrix.I
# 頂点間の距離がfMinDistよりも小さい場合は重複とみなして頂点を削除.
removeI = []
for i in range(fvCou):
p0 = vers[i]
p1 = vers[(i + 1) % fvCou]
lenV = numpy.linalg.norm(p1 - p0)
if lenV < fMinDist:
if i + 1 < fvCou:
removeI.append(i)
if len(removeI) > 0:
for i in reversed(removeI):
vers.pop(i)
versIndices.pop(i)
fvCou = len(vers)
if fvCou <= 2:
continue
# 頂点座標をZ軸向きの座標系に変換.
# この変換で、(平面上の面の場合は)Z値は0.0になる.
for i in range(fvCou):
p = vers[i]
p2 = p - fCenterPos
p2 = numpy.array([p2[0], p2[1], p2[2], 1.0])
retM = numpy.dot(p2, fnMatrixInv) # 法線座標系に変換.
p2 = [retM[0,0], retM[0,1], retM[0,2]]
vers[i] = numpy.array([p2[0], p2[1], p2[2]])
# 面の法線座標での中心 ([0, 0, 0]になる).
fCenter = numpy.array([0.0, 0.0, 0.0])
for i in range(fvCou):
fCenter += vers[i]
fCenter /= float(fvCou)
# バウンディングボックスサイズを計算.
fBBoxSize = calcBondingBoxSize(vers)
bbMinLen = min(fBBoxSize[0], fBBoxSize[1])
# lineWidthの値を調整.
lineWidth2 = min(lineWidth, bbMinLen * 0.3)
# エッジを内側にlineWidth2分シフト.
tmpVers = []
for i in range(fvCou):
e0 = i
e1 = (i + 1) % fvCou
p0 = vers[e0] - fCenter
p1 = vers[e1] - fCenter
p0_2 = numpy.array([p0[0], p0[1], 0.0])
p1_2 = numpy.array([p1[0], p1[1], 0.0])
dirV = p1_2 - p0_2
lenV = numpy.linalg.norm(dirV)
if lenV < 1e-5:
continue
dirV /= lenV
dirV2 = numpy.cross(dirV, -zUpNormal)
lenV = numpy.linalg.norm(dirV2)
if lenV < 1e-5:
continue
dirV2 /= lenV
dirV3 = dirV2 * lineWidth2
p0_3 = p0_2 + dirV3
p1_3 = p1_2 + dirV3
tmpVers.append(p0_3 + fCenter)
tmpVers.append(p1_3 + fCenter)
# エッジの交点を計算.
crossVers = []
iPos = 0
for i in range(fvCou):
p0 = tmpVers[iPos]
p1 = tmpVers[iPos + 1]
if i == 0:
iPos2 = (fvCou - 1) * 2
p0_prev = tmpVers[iPos2]
p1_prev = tmpVers[iPos2 + 1]
else:
p0_prev = tmpVers[iPos - 2]
p1_prev = tmpVers[iPos - 1]
# p0_prevを通りvDir_prevの直線と、p0を通りvDirの直線との交点を計算.
p = calcLinesCrossPos(p0, p1, p0_prev, p1_prev)
crossVers.append(p)
iPos += 2
# crossVersを元のローカル座標に戻す.
for i in range(fvCou):
p = crossVers[i]
p = numpy.array([p[0], p[1], p[2], 1.0])
retM = numpy.dot(p, fnMatrix)
p2 = numpy.array([retM[0,0], retM[0,1], retM[0,2]]) + fCenterPos
crossVers[i] = p2
newVersList.append(crossVers)
faceOrgIndicesList.append(versIndices)
if len(newVersList) >= 1:
nameStr = shape.name + '_wireframe'
scene.begin_creating()
pMesh = scene.begin_polygon_mesh(nameStr)
# オリジナルの頂点を格納.
for i in range(versCou):
p = shape.vertex(i).position
scene.append_polygon_mesh_vertex(p)
vOffset = versCou
# 新しいメッシュに頂点/面情報を格納.
fIPos = 0
fIndex = [0, 0, 0, 0]
facesCou = len(faceOrgIndicesList)
for fLoop in range(facesCou):
versOrgIndices = faceOrgIndicesList[fLoop]
newVers = newVersList[fLoop]
for p in newVers:
scene.append_polygon_mesh_vertex([p[0], p[1], p[2]])
fvCou = len(newVers)
for i in range(fvCou):
e0 = i
e1 = (i + 1) % fvCou
fIndex[0] = versOrgIndices[e0]
fIndex[1] = versOrgIndices[e1]
fIndex[2] = fIPos + e1 + vOffset
fIndex[3] = fIPos + e0 + vOffset
scene.append_polygon_mesh_face(fIndex)
fIPos += fvCou
scene.end_polygon_mesh()
pMesh.make_edges() # 稜線を生成.
pMesh.cleanup_redundant_vertices() # 重複頂点を削除.
# 面に属さない頂点を削除.
cleanupMeshVertices(pMesh)
scene.end_creating()
# 元の形状を隠す.
shape.render_flag = 0
shape.hide()
return pMesh
return None
shape = scene.active_shape()
# -------------------------------------.
# ダイアログボックスの作成.
# -------------------------------------.
dlg = xshade.create_dialog_with_uuid('5C3E7C03-B4D6-40CC-B574-24F9C31206C0')
width_id = dlg.append_float('幅', 'mm')
# デフォルトボタンを追加.
dlg.append_default_button()
# 値を指定.
dlg.set_value(width_id, 10.0)
# デフォルト値を指定.
dlg.set_default_value(width_id, 10.0)
# ダイアログボックスを表示.
if dlg.ask("ポリゴンメッシュをワイヤーフレームに変換"):
# ダイアログボックスでの値を取得.
lineWidth = dlg.get_value(width_id)
# 選択形状を取得.
shapesList = []
for shape in scene.active_shapes:
shapesList.append(shape)
# ポリゴンメッシュをワイヤーフレームに変換.
newShapesList = []
for shape in shapesList:
nShape = convMeshToWireframe(shape, lineWidth)
if nShape != None:
newShapesList.append(nShape)
if len(newShapesList) == 0:
print 'ポリゴンメッシュを選択してください。'
else:
scene.active_shapes = newShapesList
使い方
スクリプトウィンドウに、上記のコードをコピー&ペーストします。
ブラウザでポリゴンメッシュを選択します。複数選択しても動作します。
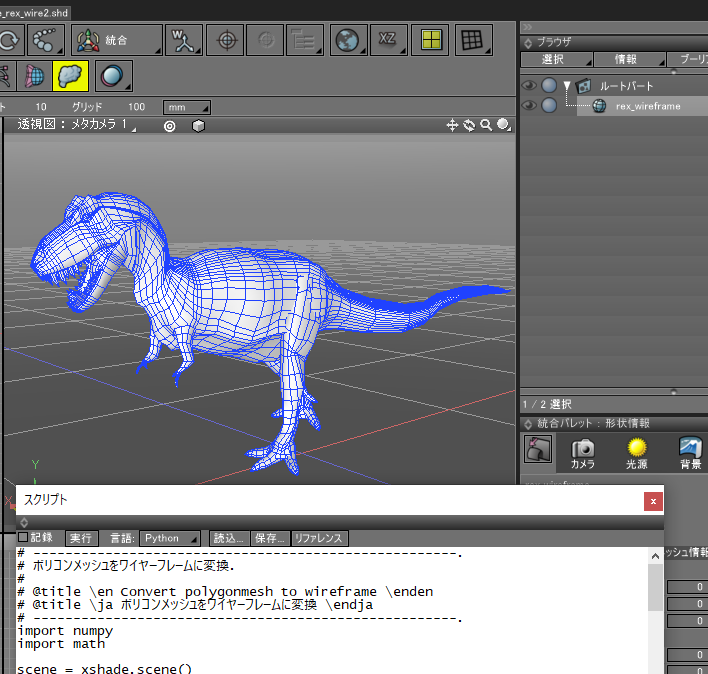
スクリプトの実行ボタンを押します。
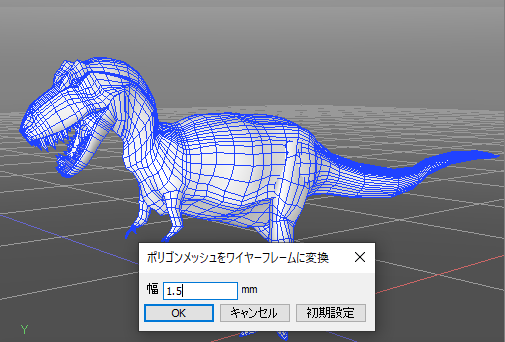
「ポリゴンメッシュをワイヤーフレームに変換」ダイアログボックスの「幅」にワイヤーフレームの幅を入力し、OKボタンを押します。
なお、面が隣接している部分は「幅 x 2」に面が貼られます。
ポリゴン数が多いほど時間がかかります。
しばらく待つと、指定の幅が最大になるようにワイヤーフレームのみのポリゴンメッシュが生成されます。
この幅より小さい面の場合は、面ごとに自動的に幅のサイズが調整されます。
元の形状は、ブラウザ上で非表示になります。
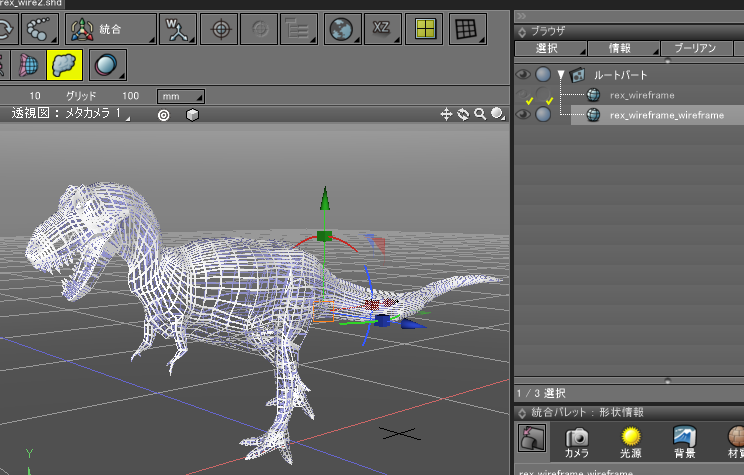
透視図でズームしていくと以下のように、元の面の内側に指定の幅の面が貼られます。

そのため、最大で「面数 x 面ごとの稜線数」の面が生成されることになります。