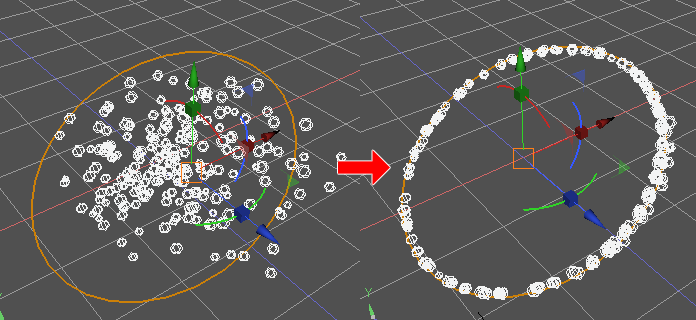
指定の線形状に沿うように選択形状を整列 (スクリプト)
指定の線形状に沿うように、選択形状を整列します。
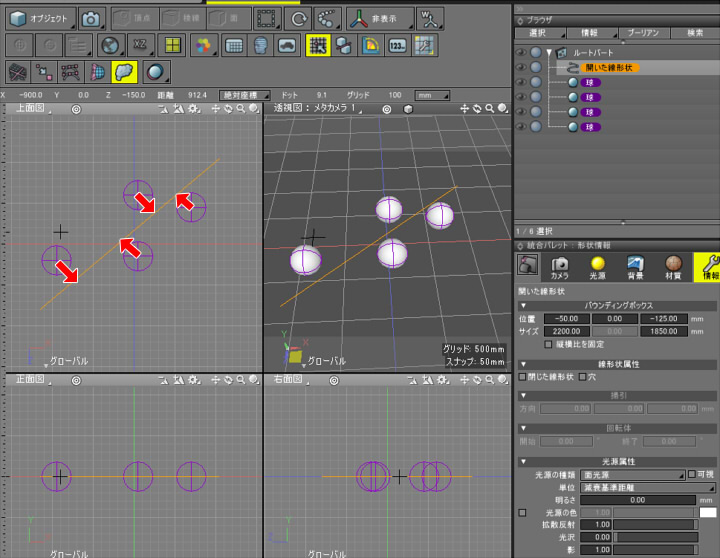
標準の機能では存在しないため、スクリプトで実現します。
import numpy
import math
scene = xshade.scene()
#---------------------------------------------------------.
# cPosがp1 - p2の直線に下す垂線情報を計算.
# @param[in] p1 直線の始点.
# @param[in] p2 直線の終点.
# @param[in] cPos 調査点.
# @param[out] retData 垂線情報が返る.
# retData = {'position': 0.0, 'distance': 0.0}
# 'position' : p1-p2を0.0-1.0としたときの位置.
# 'distance' : p1-p2に下したcPosからの垂線距離.
#---------------------------------------------------------.
def calcPerpendicular (p1, p2, cPos, retData):
retData['position'] = -1.0
retData['distance'] = -1.0
fMin = 1e-7
vDir = numpy.array([p2[0] - p1[0], p2[1] - p1[1], p2[2] - p1[2]], dtype='float64')
len1 = numpy.linalg.norm(vDir)
if len1 < fMin:
return False
vDir = vDir / len1
vDir2 = numpy.array([cPos[0] - p1[0], cPos[1] - p1[1], cPos[2] - p1[2]], dtype='float64')
len2 = numpy.linalg.norm(vDir2)
if len2 < fMin:
retData['position'] = 0.0
retData['distance'] = 0.0
return True
vDir2 = vDir2 / len2
angleV = numpy.dot(vDir, vDir2)
if math.fabs(angleV) > 1.0 - fMin:
aPos = len2 / len1
if angleV < 0.0:
retData['position'] = -aPos
retData['distance'] = 0.0
return True
len3 = angleV * len2
retData['position'] = len3 / len1
retData['distance'] = numpy.linalg.norm((vDir * len3 + p1) - cPos)
return True
#---------------------------------------.
# ゼロチェック.
#---------------------------------------.
def isZero (v):
minV = 1e-5
if v > -minV and v < minV:
return True
return False
#---------------------------------------.
# ベジェ上の位置を計算.
#---------------------------------------.
def getBezierPoint (v1Pos, v1Out, v2In, v2Pos, fPos):
fMin = 1e-6
rPos = [0.0, 0.0, 0.0]
cPos = []
cPos.append([v1Pos[0], v1Pos[1], v1Pos[2]])
cPos.append([v1Out[0], v1Out[1], v1Out[2]])
cPos.append([v2In[0], v2In[1], v2In[2]])
cPos.append([v2Pos[0], v2Pos[1], v2Pos[2]])
fPos2 = float(fPos)
fPos2 = max(0.0, fPos2)
fPos2 = min(1.0, fPos2)
if isZero(fPos2):
rPos = cPos[0]
return rPos
if isZero(fPos2 - 1.0):
rPos = cPos[3]
return rPos
# ベジェ曲線の計算.
t = fPos2
t2 = 1.0 - t
t2d = t2 * t2
td = t * t
b1 = t2d * t2
b2 = 3.0 * t * t2d
b3 = 3.0 * td * t2
b4 = t * td
for i in range(3):
rPos[i] = b1 * cPos[0][i] + b2 * cPos[1][i] + b3 * cPos[2][i] + b4 * cPos[3][i]
return rPos
#---------------------------------------.
# 線形状を直線の集まりに分解.
# @param[in] shape 対象形状.
# @param[in] lineDivCou ラインの全体の分割数.
# @return ワールド座標でのポイントの配列.
#---------------------------------------.
def getLinePoints (shape, lineDivCou):
vList = []
if shape.type != 4: # 線形状でない場合.
return vList
lwMat = numpy.matrix(shape.local_to_world_matrix)
vCou = shape.total_number_of_control_points
divCou = lineDivCou / vCou
if divCou < 4:
divCou = 4
divD = 1.0 / float(divCou)
# ベジェをポイントで保持.
for i in range(vCou):
if shape.closed == False and (i + 1 >= vCou):
break
p1 = shape.control_point(i)
p2 = shape.control_point((i + 1) % vCou)
dPos = 0.0
for j in range(divCou + 1):
p = getBezierPoint(p1.position, p1.out_handle, p2.in_handle, p2.position, dPos)
if (i == 0) or (i != 0 and j > 0):
# pをワールド座標に変換.
v = numpy.array([p[0], p[1], p[2], 1.0])
v = numpy.dot(v, lwMat)
p = [v[0,0], v[0,1], v[0,2]]
vList.append(p)
dPos += divD
return vList
#--------------------------------------------------------------.
# 指定の形状の中心座標をワールド座標で取得.
# @param[in] shape 対象形状.
#--------------------------------------------------------------.
def getShapeWorldCenterPos (shape):
cPos = shape.center_point # ローカル座標での中心座標.
lwMat = numpy.matrix(shape.local_to_world_matrix)
v = numpy.array([cPos[0], cPos[1], cPos[2], 1.0])
v = numpy.dot(v, lwMat)
cPos = [v[0,0], v[0,1], v[0,2]]
return cPos
#--------------------------------------------------------------.
# 指定の形状のワールド座標の中心を変更.
# @param[in] shape 対象形状.
# @param[in] orgWPos 元のワールド座標での中心.
# @param[in] wPos 新しいワールド座標での中心.
#--------------------------------------------------------------.
def setShapeWorldCenterPos (shape, orgWPos, wPos):
# ワールド座標位置をローカル座標に変換.
wlMat = numpy.matrix(shape.world_to_local_matrix)
v = numpy.array([orgWPos[0], orgWPos[1], orgWPos[2], 1.0])
v = numpy.dot(v, wlMat)
orgCPos = [v[0,0], v[0,1], v[0,2]]
v = numpy.array([wPos[0], wPos[1], wPos[2], 1.0])
v = numpy.dot(v, wlMat)
cPos = [v[0,0], v[0,1], v[0,2]]
# 座標の変更は、形状の移動で行う.
dV = [cPos[0] - orgCPos[0], cPos[1] - orgCPos[1], cPos[2] - orgCPos[2]]
shape.move_object(((1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (dV[0], dV[1], dV[2], 1)))
# --------------------------------------------.
# 指定の形状を、vListの線形状に近づかせる.
# @param[in] vList 線形状を分割したポイント配列.
# @param[in] shape 対象の形状.
# @param[in] distV 選択形状を記憶された線形状に近づかせる距離 (ミリメートル).
# @param[in] fMargin 範囲0.0-1.0を少しはみ出させるマージン.
# @return 処理に成功すればTrueが返る.
# --------------------------------------------.
def moveToLine (vList, shape, distV, fMargin):
# 形状のワールド座標での中心座標.
centerWPos = getShapeWorldCenterPos(shape)
# 垂線計算で使用する連想配列.
pDat = {
'position': 0.0,
'distance' : 0.0
}
# ライン上の垂線位置を計算し、一番垂線までの距離が短いところを採用.
minDist = -1.0
minPos = [0.0, 0.0, 0.0]
for i in range(len(vList) - 1):
p1 = vList[i]
p2 = vList[i + 1]
if calcPerpendicular(p1, p2, centerWPos, pDat) == False:
continue
# p1-p2を0.0-1.0としたときの位置.
pos = pDat['position']
# 垂線の足からcenterPosまでの距離.
dist = pDat['distance']
if pos < -fMargin or pos > 1.0 + fMargin:
continue
if minDist < 0.0 or dist < minDist:
minDist = dist
# 垂線の足を計算.
np1 = numpy.array([p1[0], p1[1], p1[2]], dtype='float64')
np2 = numpy.array([p2[0], p2[1], p2[2]], dtype='float64')
minPos = (np2 - np1) * pos + np1
if minDist >= 0.0:
cPos = numpy.array([centerWPos[0], centerWPos[1], centerWPos[2]], dtype='float64')
vDir = cPos - minPos
# 垂線の足(minPos)からdistVだけ離れた位置を計算.
lenV = numpy.linalg.norm(vDir)
if lenV != 0.0:
vDir /= lenV
if lenV > distV:
newPos = vDir * distV + minPos
# 中心位置を更新.
setShapeWorldCenterPos(shape, centerWPos, [newPos[0], newPos[1], newPos[2]])
return True
return False
# ---------------------------------------------------------------------.
# 範囲0.0-1.0を少しはみ出させるマージン.
fMargin = 0.5
if scene.number_of_memorized_shapes == 0 or scene.memorized_shape().type != 4:
xshade.show_message_box('線形状を「記憶」してください。', False)
else:
# 記憶された形状を取得.
memShape = scene.memorized_shape()
if memShape.type == 4: # 線形状の場合.
# ダイアログボックスの作成と表示.
dlg = xshade.create_dialog_with_uuid('5ac13729-57cb-4777-ba0b-644d3f1daca0')
div_id = dlg.append_int('線形状の分割数')
dist_id = dlg.append_float('線形状から離す距離', 'mm')
dlg.set_value(div_id, 50)
dlg.set_value(dist_id, 10.0)
dlg.set_default_value(div_id, 50)
dlg.set_default_value(dist_id, 10.0)
dlg.append_default_button()
if dlg.ask("選択形状を記憶した線形状に整列"):
lineDivCou = max(10, dlg.get_value(div_id))
distV = max(0.0, dlg.get_value(dist_id))
# 選択形状を取得し、線形状以外のものを格納.
aShapes = []
for shape in scene.active_shapes:
if shape.type != 4:
aShapes.append(shape)
for loop in range(3):
# 線形状からポイントの配列を取得.
vList = getLinePoints(memShape, lineDivCou)
updateF = False
for i in range(len(aShapes)):
if aShapes[i] == None:
continue
# 指定の形状を、memShape(vListがポイントの配列)の線形状に近づかせる.
if moveToLine(vList, aShapes[i], distV, fMargin):
aShapes[i] = None
updateF = True
if updateF == False:
break
# 線分上に垂線が存在しない場合は、ラインの分割を粗くして再度行う.
lineDivCou /= 2
使い方は、
線形状を選択しツールパラメータの「記憶」ボタンを押して形状を記憶します。
線形状に寄せる形状をブラウザで選択し、上記スクリプトを実行します。
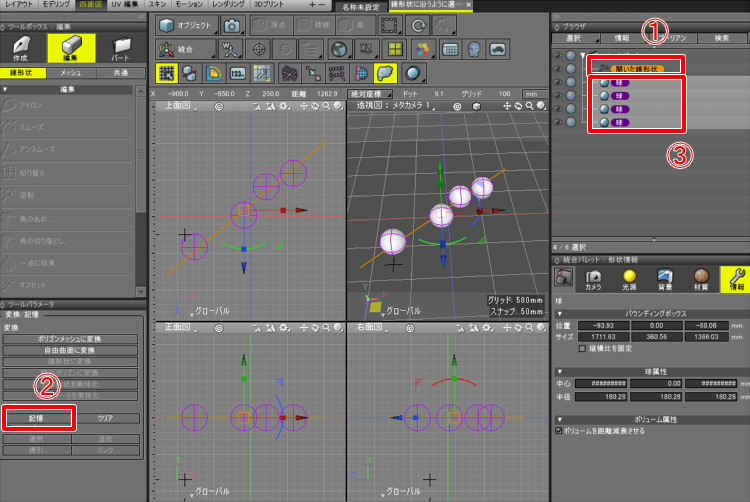
実行すると、ダイアログボックスにパラメータが表示されます。
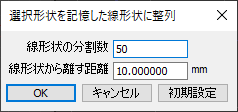
「線形状の分割数」は記憶した線形状を内部的に何分割するか整数で指定し、
「線形状から離す距離」は線形状からどれだけ離すかを指定します。
ダイアログボックスでOKボタンを押して確定すると、
選択形状が記憶した線形状に沿って垂線が「線形状から離す距離」の距離だけ離れた位置に移動します。
なお、このスクリプトはUNDO/REDOには対応していません。
以下のように曲線に対しても使用できます。