線形状に沿ってチューブ状のポリゴンメッシュを作成 (スクリプト)
Standard/Professionalのグレードの場合は、プラグインとしての「掃引-円」機能を使うことで、
線形状を中心としたチューブ形状の作成ができます。
Basic版ではこの機能は使えないため、スクリプトで補助します。
import numpy
import math
scene = xshade.scene()
#---------------------------------------.
# ゼロチェック.
#---------------------------------------.
def isZero (v):
minV = 1e-5
if v > -minV and v < minV:
return True
return False
#---------------------------------------.
# ベジェ上の位置を計算.
#---------------------------------------.
def getBezierPoint (v1Pos, v1Out, v2In, v2Pos, fPos):
fMin = 1e-6
rPos = [0.0, 0.0, 0.0]
cPos = []
cPos.append([v1Pos[0], v1Pos[1], v1Pos[2]])
cPos.append([v1Out[0], v1Out[1], v1Out[2]])
cPos.append([v2In[0], v2In[1], v2In[2]])
cPos.append([v2Pos[0], v2Pos[1], v2Pos[2]])
fPos2 = float(fPos)
fPos2 = max(0.0, fPos2)
fPos2 = min(1.0, fPos2)
if isZero(fPos2):
rPos = cPos[0]
return rPos
if isZero(fPos2 - 1.0):
rPos = cPos[3]
return rPos
# ベジェ曲線の計算.
t = fPos2
t2 = 1.0 - t
t2d = t2 * t2
td = t * t
b1 = t2d * t2
b2 = 3.0 * t * t2d
b3 = 3.0 * td * t2
b4 = t * td
for i in range(3):
rPos[i] = b1 * cPos[0][i] + b2 * cPos[1][i] + b3 * cPos[2][i] + b4 * cPos[3][i]
return rPos
#---------------------------------------.
# 線形状を直線の集まりに分解.
# @param[in] shape 対象形状.
# @param[in] lineDivCou ラインの全体の分割数.
# @return ポイントの配列.
#---------------------------------------.
def getLinePoints (shape, lineDivCou):
vCou = shape.total_number_of_control_points
vList = []
if shape.type != 4 or vCou < 2: # 線形状でない場合.
return vList
divCou = lineDivCou / vCou
if divCou < 4:
divCou = 4
divD = 1.0 / float(divCou)
# ベジェをポイントで保持.
for i in range(vCou):
if shape.closed == False and (i + 1 >= vCou):
break
p1 = shape.control_point(i)
p2 = shape.control_point((i + 1) % vCou)
dPos = 0.0
for j in range(divCou + 1):
p = getBezierPoint(p1.position, p1.out_handle, p2.in_handle, p2.position, dPos)
if (i == 0) or (i != 0 and j > 0):
vList.append(p)
dPos += divD
return vList
#---------------------------------------.
# ポイントのみで構成された配列情報から、等間隔になるように再計算.
# @param[in] vList ポイントの配列.
# @param[in] divCou 新しいラインの分割数.
# @return ポイントの配列.
#---------------------------------------.
def recalcLinePoints (vList, divCou):
# numpyの形式に配列に格納し直す.
vListLen = len(vList)
if vListLen < 2:
return []
posA = []
for i in range(vListLen):
posA.append(numpy.array([vList[i][0], vList[i][1], vList[i][2]]))
# ラインの長さを計算.
allLen = 0.0
lenList = []
for i in range(vListLen - 1):
vLen = numpy.linalg.norm(posA[i + 1] - posA[i])
lenList.append(vLen)
allLen += vLen
dLen = allLen / (divCou - 1.0)
newPosA = []
newPosA.append([posA[0][0], posA[0][1], posA[0][2]])
dPos = 0.0
for i in range(vListLen - 1):
len1 = lenList[i]
if dPos + len1 < dLen:
dPos += len1
continue
dPos2 = 0.0
while dPos2 < len1:
dd = (dPos2 + (dLen - dPos)) / len1
p = (posA[i + 1] - posA[i]) * dd + posA[i]
newPosA.append([p[0], p[1], p[2]])
if len(newPosA) >= divCou - 1:
break
dd2 = dLen - dPos
if dPos2 + dd2 + dLen > len1:
dPos = len1 - (dPos2 + dd2)
break
dPos2 += dd2
dPos = 0.0
if len(newPosA) >= divCou - 1:
break
newPosA.append([posA[-1][0], posA[-1][1], posA[-1][2]])
return newPosA
#---------------------------------------.
# ベクトルの単位ベクトルを計算.
#---------------------------------------.
def calcVecNormal (vD):
vD2 = vD
lenV = numpy.linalg.norm(vD2)
if lenV != 0.0:
vD2 /= lenV
return vD2
#---------------------------------------.
# 指定の進行方向から行列を作成.
# @param[in] vDir 進行方向のベクトル.
# @return 進行方向をZとしたときの4x4行列を返す.
#---------------------------------------.
def calcDirToMatrix (vDir):
vDir0 = calcVecNormal(vDir)
m = numpy.matrix(numpy.identity(4))
vX = numpy.array([1.0, 0.0, 0.0])
vY = numpy.array([0.0, 1.0, 0.0])
dirY = vY
angleV = numpy.dot(vDir0, vY)
if math.fabs(angleV) > 0.999:
dirY = vX
dirX = numpy.cross(vDir0, dirY)
dirX = calcVecNormal(dirX)
dirY = numpy.cross(dirX, vDir0)
dirY = calcVecNormal(dirY)
m[0, 0] = dirX[0]
m[0, 1] = dirX[1]
m[0, 2] = dirX[2]
m[1, 0] = dirY[0]
m[1, 1] = dirY[1]
m[1, 2] = dirY[2]
m[2, 0] = vDir0[0]
m[2, 1] = vDir0[1]
m[2, 2] = vDir0[2]
return m
# -------------------------------------------------------.
shape = scene.active_shape()
if shape.type != 4 or shape.total_number_of_control_points < 2:
xshade.show_message_box('ポイント数が2以上の線形状を選択してください。', False)
else:
# ダイアログボックスの作成と表示.
dlg = xshade.create_dialog_with_uuid('1cb3c17f-6df6-4451-ab9e-473034179357')
divU_id = dlg.append_int('分割数 U (円周まわり)')
divV_id = dlg.append_int('分割数 V (線形状の進行方向)')
startRadius_id = dlg.append_float('開始半径', 'mm')
endRadius_id = dlg.append_float('終了半径', 'mm')
dlg.set_value(divU_id, 12)
dlg.set_value(divV_id, 10)
dlg.set_value(startRadius_id, 100.0)
dlg.set_value(endRadius_id, 100.0)
dlg.set_default_value(divU_id, 12)
dlg.set_default_value(divV_id, 10)
dlg.set_default_value(startRadius_id, 100.0)
dlg.set_default_value(endRadius_id, 100.0)
dlg.append_default_button()
if dlg.ask("線形状からポリゴンメッシュのチューブを作成"):
divVCou = max(2, dlg.get_value(divV_id) + 1)
divUCou = max(3, dlg.get_value(divU_id) + 1)
startRadiusV = max(0.001, dlg.get_value(startRadius_id))
endRadiusV = max(0.001, dlg.get_value(endRadius_id))
# 線形状をポイントで分割.
divCou = min(40, divVCou * 4)
vList = getLinePoints(shape, divCou)
vList2 = recalcLinePoints(vList, divVCou)
if shape.closed:
vList2.pop()
# ---------------------------------------------------.
# ポリゴンメッシュのチューブを作成.
# ---------------------------------------------------.
scene.begin_creating()
mesh = scene.begin_polygon_mesh(None)
# numpyのポイントの形で再格納.
vListCou = len(vList2)
for i in range(vListCou):
p = vList2[i]
vList2[i] = numpy.array([p[0], p[1], p[2]], dtype = 'float64')
# +Zを中心とした半径radiusVのポイントを計算.
circleV = []
dd = (math.pi * 2.0) / ((float)(divUCou))
dPos = 0.0
for i in range(divUCou):
circleV.append(numpy.array([math.cos(dPos), math.sin(dPos), 0.0], dtype = 'float64'))
dPos += dd
# ポリゴンメッシュのポイントを配置.
m = numpy.matrix(numpy.identity(4))
vDir0 = numpy.array([0.0, 0.0, 1.0])
radiusV = startRadiusV
radiusD = (endRadiusV - startRadiusV) / (float)(vListCou - 1)
for i in range(vListCou):
if shape.closed == False and i + 1 >= vListCou:
p1 = vList2[i]
else:
p1 = vList2[i]
p2 = vList2[(i + 1) % vListCou]
vDir = calcVecNormal(p2 - p1)
if i == 0:
m = calcDirToMatrix(p2 - p1)
vDir0 = vDir
else:
pV0 = numpy.dot(numpy.array([vDir0[0], vDir0[1], vDir0[2], 1.0]), m.I)
pV0 = numpy.array([pV0[0,0], pV0[0,1], pV0[0,2]])
pV1 = numpy.dot(numpy.array([vDir[0], vDir[1], vDir[2], 1.0]), m.I)
pV1 = numpy.array([pV1[0,0], pV1[0,1], pV1[0,2]])
m0 = calcDirToMatrix(pV0)
m1 = calcDirToMatrix(pV1)
m = (m1.I * m0).I * m
for j in range(divUCou):
p = circleV[j]
p = numpy.dot(numpy.array([p[0] * radiusV, p[1] * radiusV, p[2] * radiusV, 1.0]), m)
p = [p[0,0] + p1[0], p[0,1] + p1[1], p[0,2] + p1[2]]
scene.append_polygon_mesh_vertex(p)
vDir0 = vDir
radiusV += radiusD
# ポリゴンメッシュの面を配置.
iPos = 0
vCou = vListCou - 1
if shape.closed:
vCou = vListCou
for i in range(vCou):
for j in range(divUCou):
i0 = iPos + j
i1 = iPos + ((j + 1) % divUCou)
if shape.closed and i + 1 >= vListCou:
i2 = ((j + 1) % divUCou)
i3 = j
else:
i2 = iPos + divUCou + ((j + 1) % divUCou)
i3 = iPos + divUCou + j
scene.append_polygon_mesh_face([i3, i2, i1, i0])
iPos += divUCou
# 稜線を計算.
scene.append_polygon_mesh_edges()
# UVの割り当て.
uvIndex = mesh.append_uv_layer()
uD = 1.0 / (float)(divUCou)
vD = 1.0 / (float)(divVCou - 1)
faceI = 0
vPos = 0.0
for i in range(vCou):
uPos = 0.0
for j in range(divUCou):
f = mesh.face(faceI)
f.set_face_uv(uvIndex, 3, [1.0 - uPos, 1.0 - vPos])
f.set_face_uv(uvIndex, 2, [1.0 - (uPos + uD), 1.0 - vPos])
f.set_face_uv(uvIndex, 1, [1.0 - (uPos + uD), 1.0 - (vPos + vD)])
f.set_face_uv(uvIndex, 0, [1.0 - uPos, 1.0 - (vPos + vD)])
faceI = faceI + 1
uPos += uD
vPos += vD
scene.end_polygon_mesh()
scene.end_creating()
線形状を選択し上記スクリプトを実行すると、以下のダイアログボックスが表示されます。
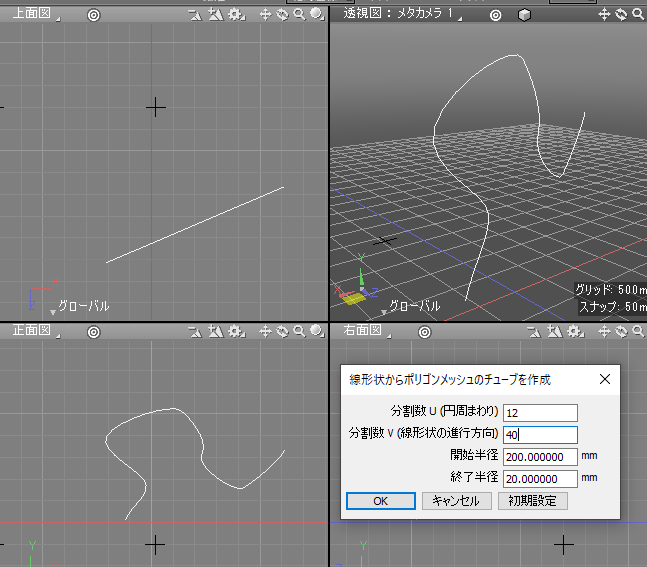
「分割数 U」は生成するチューブ形状の円周回りの分割数です。
「分割数 V」は生成するチューブ形状の進行方向での分割数です。
「開始半径」は生成するチューブ形状の開始位置での半径です。
「終了半径」は生成するチューブ形状の終了位置での半径です。
OKボタンを押すと、線形状を中心としたポリゴンメッシュのチューブ形状が生成されます。
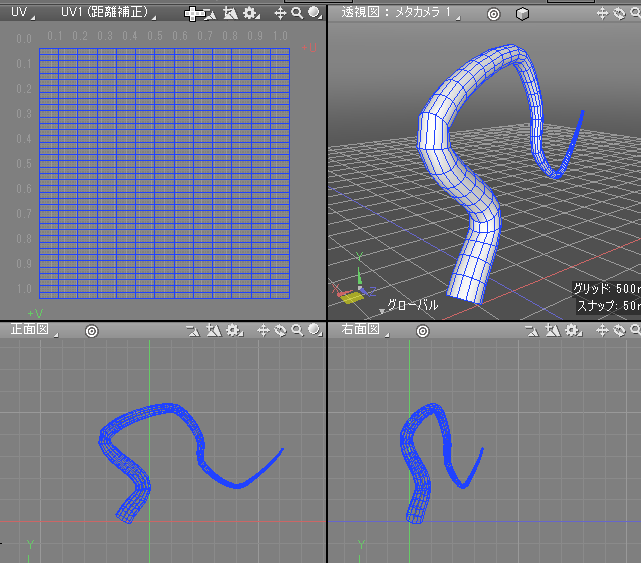
UV1のUV層に対して、U方向にチューブ形状の円周回り、V方向にチューブ形状の進行方向でUVが割り当てられます。